The OpenMS kernel contains the data structures that store the actual MS data, i.e. raw data points, peaks, features, spectra, maps. The classes described in this section can be found in the KERNEL folder.

Raw data point, Peak, Feature, ...

In general, there are three types of data points: raw data points, peaks and picked peaks. Raw data points provide members to store position (mass-to-charge ratio, retention time, ...) and intensity. Peaks are derived from raw data points and add an interface to store meta information. Picked peaks are derived from peaks and have additional members for peak shape information: charge, width, signal-to-noise ratio and many more.

The kernel data points exist in three versions: one-dimensional, two-dimensional and d-dimensional.

Data structures for MS data points

one-dimensional data points: The one-dimensional data points are most important, the two-dimensional and d-dimensional data points are needed rarely. The base class of the one-dimensional data points is Peak1D. It provides members to store the mass-to-charge ratio (getMZ and setMZ) and the intensity (getIntensity and setIntensity).
RichPeak1D is derived from Peak1D and adds an interface for metadata (see MetaInfo).

two-dimensional data points: The two-dimensional data points are needed when geometry algorithms are applied to the data points. A special case is the Feature class, which needs a two-dimensional position (m/z and RT).
The base class of the two-dimensional data points is Peak2D. It provides the same interface as Peak1D and additional members for the retention time (getRT and setRT).
RichPeak2D is derived from Peak2D and adds an interface for metadata.
Feature is derived from RichPeak2D and adds information about the convex hull of the feature, fitting quality and so on.

d-dimensional data points: The d-dimensional data points are needed only in special cases, e.g. in template classes that must operate on any number of dimensions.
The base class of the d-dimensional data points is DPeak. The methods to access the position are getPosition and setPosition.
Note that the one-dimensional and two-dimensional data points also have the methods getPosition and setPosition. They are needed in order to be able to write algorithms that can operate on all data point types. It is, however, recommended not to use these members unless you really write such a generic algorithm.

Spectra

The most important container for raw data and peaks is MSSpectrum. It is a template class that takes the peak type as template argument. The default peak type is RichPeak1D. Possible other peak types are classes derived from Peak1D or classes providing the same interface.
MSSpectrum is a container for 1-dimensional peak data. It is derived from SpectrumSettings, a container for the meta data of a spectrum. Here, only MS data handling is explained, SpectrumSettings is described in section Meta data of a spectrum.

In the following example (Tutorial_MSSpectrum.cpp) program, a MSSpectrum is filled with peaks, sorted according to mass-to-charge ratio and a selection of peak positions is displayed.

First we create a spectrum and insert peaks with descending mass-to-charge ratios:

Int main()
{
  MSSpectrum spectrum;
  Peak1D peak;
  for (float mz = 1500.0; mz >= 500; mz -= 100.0)
  {
    peak.setMZ(mz);
    spectrum.push_back(peak);
  }

Then we sort the peaks according to ascending mass-to-charge ratio.

spectrum.sortByPosition();

Finally we print the peak positions of those peaks between 800 and 1000 Thomson. For printing all the peaks in the spectrum, we simply would have used the STL-conform methods begin() and end().

  // iterate between range
  MSSpectrum::Iterator it;
  for (it = spectrum.MZBegin(800.0); it != spectrum.MZEnd(1000.0); ++it)
  {
    cout << it->getMZ() << endl;
  }
  return 0;
} //end of main

Typedefs: For convenience, the following type definitions are defined in OpenMS/KERNEL/StandardTypes.h.
typedef MSSpectrum<RichPeak1D> RichPeakSpectrum;
typedef MSSpectrum<Peak1D> PeakSpectrum;

Maps

Although raw data maps, peak maps and feature maps are conceptually very similar. They are stored in different data types. For raw data and peak maps, the default container is MSExperiment, which is an array of MSSpectrum instances. Just as MSSpectrum it is a template class with the peak type as template parameter.

In contrast to raw data and peak maps, feature maps are no collection of one-dimensional spectra, but an array of two-dimensional Feature instances. The main data structure for feature maps is called FeatureMap.

Although MSExperiment and FeatureMap differ in the data they store, they also have things in common. Both store meta data that is valid for the whole map, i.e. sample description and instrument description. This data is stored in the common base class ExperimentalSettings.

MSExperiment: The following figure shows the big picture of the kernel data structures. MSExperiment is derived from ExperimentalSettings (meta data of the experiment) and contains two data vectors, available as vector<MSSpectrum> and vector<MSChromatogram>. The one-dimensional spectrum MSSpectrum is derived from SpectrumSettings (meta data of a spectrum.

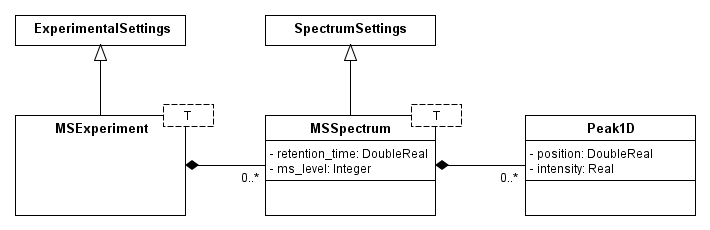Overview of the main kernel data structures

The following example program (Tutorial_MSExperiment.cpp) creates a MSExperiment containing four MSSpectrum instances. Then it iterates over an area and prints the peak positions in the area:

First we create the spectra in a for-loop and set the retention time and MS level. Survey scans have a MS level of 1, MS/MS scans would have a MS level of 2, and so on.

Int main()
{
  PeakMap exp;
  for (Size i = 0; i < 4; ++i)
  {
    PeakSpectrum spectrum;
    spectrum.setRT(i);
    spectrum.setMSLevel(1);

Then we fill each spectrum with several peaks. As all spectra would have the same peaks otherwise, we add the retention time to the mass-to-charge ratio of each peak.

    for (float mz = 500.0; mz <= 900; mz += 100.0)
    {
      Peak1D peak;
      peak.setMZ(mz + i);
      spectrum.push_back(peak);
    }
    exp.addSpectrum(spectrum);
  } //end of creation

Finally, we iterate over the RT range (2,3) and the m/z range (603,802) and print the peak positions.

  for (PeakMap::AreaIterator it = exp.areaBegin(2.0, 3.0, 603.0, 802.0); it != exp.areaEnd(); ++it)
  {
    cout << it.getRT() << " - " << it->getMZ() << endl;
  }

The output of this loop is:

For printing all the peaks in the experiment, we could have used the STL-iterators of the experiment to iterate over the spectra and the STL-iterators of the spectra to iterate over the peaks:

  for (PeakMap::Iterator s_it = exp.begin(); s_it != exp.end(); ++s_it)
  {
    for (PeakSpectrum::Iterator p_it = s_it->begin(); p_it != s_it->end(); ++p_it)
    {
      cout << s_it->getRT() << " - " << p_it->getMZ() << endl;
    }
  }
  return 0;
} //end of main

FeatureMap: FeatureMap, the container for features, is simply a vector<Feature>. Additionally, it is derived from ExperimentalSettings, to store the meta information. Just like MSExperiment, it is a template class. It takes the feature type as template argument.

The following example (Tutorial_FeatureMap.cpp) shows how to insert two features into a map and iterate over the features.

Int main()
{
  FeatureMap map;
  Feature feature;
  feature.setRT(15.0);
  feature.setMZ(571.3);
  map.push_back(feature); //append feature 1
  feature.setRT(23.3);
  feature.setMZ(1311.3);
  map.push_back(feature); //append feature 2
  for (FeatureMap::Iterator it = map.begin(); it != map.end(); ++it)
  {
    cout << it->getRT() << " - " << it->getMZ() << endl;
  }
  return 0;
} //end of main

RangeManager: All peak and feature containers (MSSpectrum, MSExperiment, FeatureMap) are also derived from RangeManager. This class facilitates the handling of MS data ranges. It allows to calculate and store both the position range and the intensity range of the container.

The following example (Tutorial_RangeManager.cpp) shows the functionality of the class RangeManger using a FeatureMap. First a FeatureMap with two features is created, then the ranges are calculated and printed:

Int main()
{
  FeatureMap map;
  Feature feature;
  feature.setIntensity(461.3f);
  feature.setRT(15.0);
  feature.setMZ(571.3);
  map.push_back(feature);
  feature.setIntensity(12213.5f);
  feature.setRT(23.3);
  feature.setMZ(1311.3);
  map.push_back(feature);
  //calculate the ranges
  map.updateRanges();
  cout << "Int: " << map.getMinInt() << " - " << map.getMaxInt() << endl;
  cout << "RT:  " << map.getMin()[0] << " - " << map.getMax()[0] << endl;
  cout << "m/z: " << map.getMin()[1] << " - " << map.getMax()[1] << endl;
  return 0;
} //end of main

The output of this program is:

Int: 461.3 - 12213.5
RT:  15 - 23.3
m/z: 571.3 - 1311.3